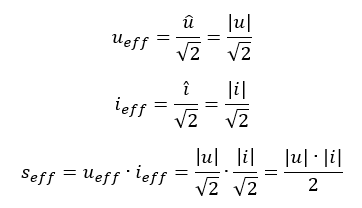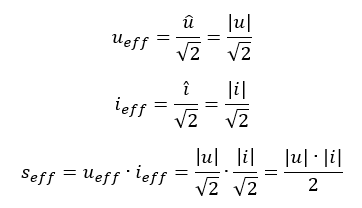Komplexe Leistung (Elektrotechnik)

Die komplexe Leistung (auch komplexe Scheinleistung) ist eine Rechengröße der Elektrotechnik, welche die verschiedenen Leistungskennwerte bei Wechselstrom zu einem Wert zusammenfasst, welcher mit der symbolischen Methode der komplexen Wechselstromrechnung vereinbar ist. Die Bezeichnung resultiert daraus, dass dieser Wert eine komplexe Zahl ist.

Motivation

Die komplexe Wechselstromrechnung ist, wie dort gezeigt wird, nur für lineare Rechenoperationen geeignet. Sie versagt beispielsweise bei der Multiplikation von komplexer Spannung und komplexem Strom. Im Gegensatz zur Momentanleistung ${\displaystyle u(t)\cdot i(t)}$ und zur Scheinleistung ${\displaystyle U\cdot I}$ hat deshalb das entsprechende Produkt ${\displaystyle {\underline {u}}(t)\cdot {\underline {i}}(t)}$ genauso wie das Produkt aus den komplexen Effektivwerten ${\displaystyle {\underline {U}}\cdot {\underline {I}}}$ keinen praktischen Sinn. Wenn man jedoch eine komplexe Spannung mit einem konjugiert komplexen Strom multipliziert, heben sich die zeitabhängigen Teile ${\displaystyle \mathrm {e} ^{\mathrm {j} \omega t}}$ und ${\displaystyle \mathrm {e} ^{-\mathrm {j} \omega t}}$ gegenseitig auf und es geht nur die gegenseitige Phasenverschiebung ein. Das motiviert zur folgenden Definition.

Definition

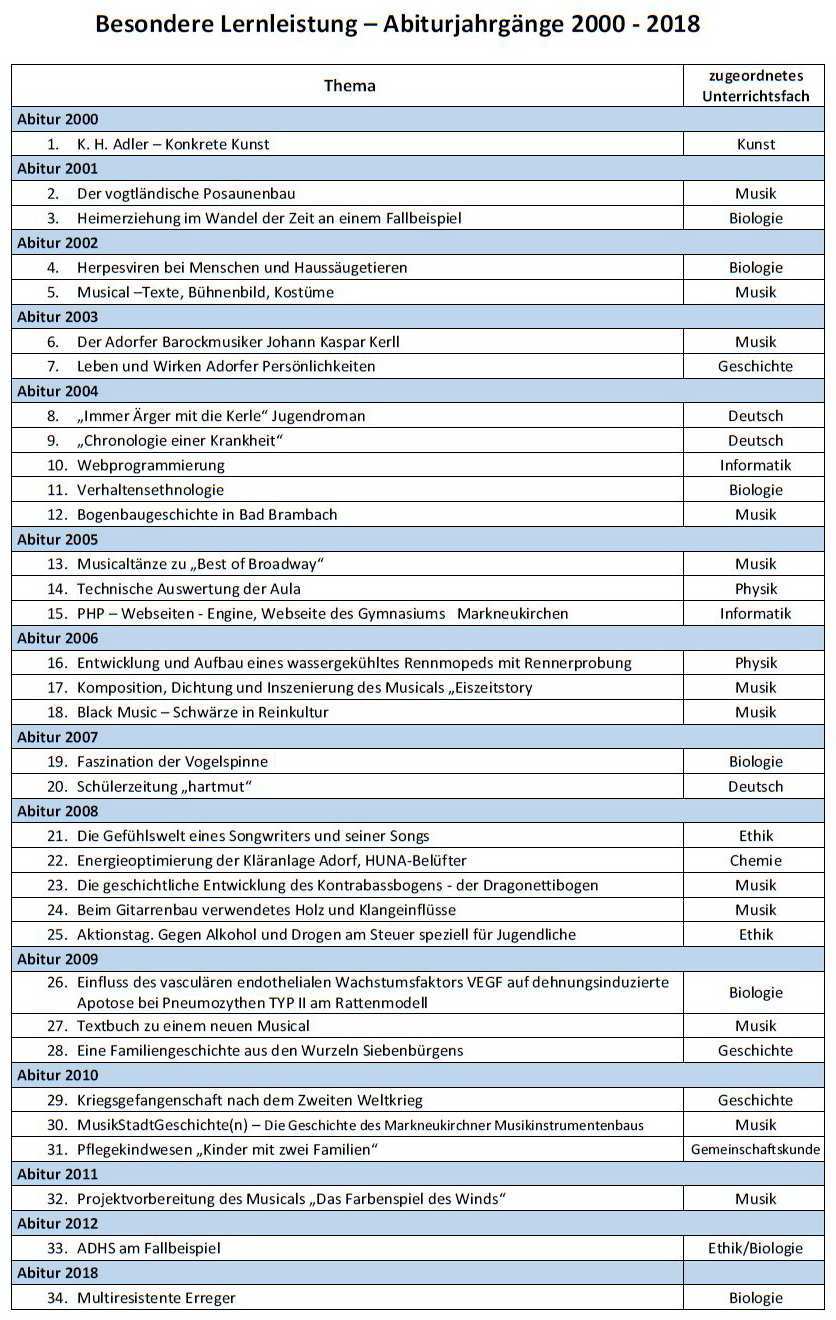
Als komplexe Leistung ${\displaystyle {\underline {S}}}$ an einem Zweipol definiert man das Produkt aus komplexem Effektivwert der Spannung ${\displaystyle {\underline {U}}=U\cdot \mathrm {e} ^{\mathrm {j} \varphi _{u}}}$ und konjugiert komplexem Effektivwert des Stromes ${\displaystyle {\underline {I}}^{\star }=I\cdot \mathrm {e} ^{-\mathrm {j} \varphi _{i}}}$. Da die Amplituden um ${\displaystyle {\sqrt {2}}}$ größer als die Effektivwerte sind, ist die komplexe Leistung damit gleich dem halben Produkt aus komplexer Amplitude der Spannung und konjugiert komplexer Amplitude des Stromes:

${\displaystyle {\underline {S}}={\underline {U}}\cdot {\underline {I}}^{\star }={\frac {{\underline {\hat {u}}}\cdot {\underline {\hat {\imath }}}^{\star }}{2}}}$

Durch die ausführliche Schreibweise

${\displaystyle {\underline {S}}={\underline {U}}\cdot {\underline {I}}^{\star }=U\cdot \mathrm {e} ^{ \mathrm {j} \varphi _{u}}\cdot I\cdot \mathrm {e} ^{-\mathrm {j} \varphi _{i}}=U\cdot I\cdot \mathrm {e} ^{\mathrm {j} (\varphi _{u}-\varphi _{i})}=U\cdot I\cdot {\bigl (}\cos(\varphi _{u}-\varphi _{i}) \mathrm {j} \sin(\varphi _{u}-\varphi _{i}){\bigr )}}$

und die übliche Abkürzung ${\displaystyle \varphi =\varphi _{u}-\varphi _{i}}$ für die Phasenverschiebung sowie die Aufspaltung in Real- und Imaginärteil

${\displaystyle {\underline {S}}=S\cdot \mathrm {e} ^{\mathrm {j} \varphi }=S\cdot \left(\cos \varphi \mathrm {j} \sin \varphi \right)=P \mathrm {j} Q}$

wird deutlich, wie die in der Wechselstromtechnik üblichen drei Kenngrößen der Leistung mit der komplexen Leistung zusammen hängen:

• Die Wirkleistung ${\displaystyle P}$ ist der Realteil der komplexen Leistung:

${\displaystyle P=\mathrm {Re} \ {\underline {S}}=S\cdot \cos \varphi =U\cdot I\cdot \cos \varphi }$

• Die (Verschiebungs-)Blindleistung ${\displaystyle Q}$ ist der Imaginärteil der komplexen Leistung:

${\displaystyle Q=\mathrm {Im} \ {\underline {S}}=S\cdot \sin \varphi =U\cdot I\cdot \sin \varphi }$

• Die Scheinleistung ${\displaystyle S}$ ist der Betrag der komplexen Leistung

${\displaystyle S=\left|{\underline {S}}\right|=U\cdot I={\sqrt {P^{2} Q^{2}}}}$

Hat beispielsweise die Spannung die Amplitude ${\displaystyle {\hat {u}}=10\ {\text{V}}}$ und den Nullphasenwinkel ${\displaystyle \varphi _{u}=-30^{\circ }}$ sowie der Strom die Amplitude ${\displaystyle {\hat {\imath }}=8\ {\text{A}}}$ und den Nullphasenwinkel ${\displaystyle \varphi _{i}=0^{\circ }}$, dann erhält man für die komplexe Leistung

${\displaystyle {\underline {S}}=40\ {\text{VA}}\cdot \mathrm {e} ^{-\mathrm {j} \cdot 30^{\circ }}=40\ {\text{VA}}\cdot \left(\cos(-30^{\circ }) \mathrm {j} \cdot \sin(-30^{\circ })\right)\approx 34,64\ {\text{W}}-\mathrm {j} \cdot 20\ {\text{var}}}$

mit der Wirkleistung ${\displaystyle P=34,64\ {\text{W}}}$ und der Blindleistung ${\displaystyle Q=-20\ {\text{var}}}$. Sofern Strom und Spannung dem Verbraucherzählpfeilsystem entstammen, handelt es sich bei diesem Zweipol also um einen kapazitiven (${\displaystyle Q<0}$) Verbraucher (${\displaystyle P>0}$).

Komplexe Leistung an passiven Zweipolen

Sind die Stromstärke und die Impedanz oder Admittanz eines passiven (linearen) Zweipols gegeben, dann gilt (unter Annahme des Verbraucherzählpfeilsystems) mit ${\displaystyle {\underline {U}}={\underline {Z}}\cdot {\underline {I}}={\frac {\underline {I}}{\underline {Y}}}}$ für die komplexe Leistung

${\displaystyle {\underline {S}}={\underline {Z}}\cdot I^{2}={\frac {I^{2}}{\underline {Y}}}={\frac {{\underline {Z}}\cdot {\hat {\imath }}^{2}}{2}}={\frac {{\hat {\imath }}^{2}}{2\ {\underline {Y}}}}}$

Sind dagegen die Spannung und die Impedanz oder Admittanz gegeben, dann gilt mit ${\displaystyle {\underline {I}}={\underline {Y}}\cdot {\underline {U}}={\frac {\underline {U}}{\underline {Z}}}}$

${\displaystyle {\underline {S}}={\underline {Y}}^{\star }\cdot U^{2}={\frac {U^{2}}{{\underline {Z}}^{\star }}}={\frac {{\underline {Y}}^{\star }\cdot {\hat {u}}^{2}}{2}}={\frac {{\hat {u}}^{2}}{2\ {\underline {Z}}^{\star }}}}$

Damit erhält man für Wirk-, Blind- und Scheinleistung

${\displaystyle P=\mathrm {Re} \ {\underline {S}}=I^{2}\cdot \mathrm {Re} \ {\underline {Z}}=U^{2}\cdot \mathrm {Re} \ {\underline {Y}}={\frac {{\hat {\imath }}^{2}}{2}}\cdot \mathrm {Re} \ {\underline {Z}}={\frac {{\hat {u}}^{2}}{2}}\cdot \mathrm {Re} \ {\underline {Y}}}$

${\displaystyle Q=\mathrm {Im} \ {\underline {S}}=I^{2}\cdot \mathrm {Im} \ {\underline {Z}}=-U^{2}\cdot \mathrm {Im} \ {\underline {Y}}={\frac {{\hat {\imath }}^{2}}{2}}\cdot \mathrm {Im} \ {\underline {Z}}=-{\frac {{\hat {u}}^{2}}{2}}\cdot \mathrm {Im} \ {\underline {Y}}}$

${\displaystyle S=\left|{\underline {S}}\right|=I^{2}\cdot \left|{\underline {Z}}\right|=U^{2}\cdot \left|{\underline {Y}}\right|={\frac {U^{2}}{\left|{\underline {Z}}\right|}}={\frac {I^{2}}{\left|{\underline {Y}}\right|}}={\frac {{\hat {\imath }}^{2}}{2}}\cdot \left|{\underline {Z}}\right|={\frac {{\hat {u}}^{2}}{2}}\cdot \left|{\underline {Y}}\right|={\frac {{\hat {u}}^{2}}{2\ \left|{\underline {Z}}\right|}}={\frac {{\hat {\imath }}^{2}}{2\ \left|{\underline {Y}}\right|}}}$

Als Beispiel erhält man für die Blindleistung eines Kondensators mit der Kapazität ${\displaystyle C}$ an einer Spannung mit der Amplitude ${\displaystyle {\hat {u}}}$ und der Kreisfrequenz ${\displaystyle \omega }$

${\displaystyle Q=-{\frac {{\hat {u}}^{2}\cdot \omega \ C}{2}}}$

Konkret entsteht bei ${\displaystyle 230\ {\text{V}}}$ und ${\displaystyle 50\ {\text{Hz}}}$ an einem Kondensator mit einer Kapazität von ${\displaystyle 100\ {\text{nF}}}$ eine Blindleistung von ${\displaystyle Q\approx -1,66\ {\text{var}}}$.

Zusammenhang der komplexen Leistung mit der Momentanleistung

Der Energiefluss in einen Zweipol wird durch den Momentanwert der elektrischen Leistung ${\displaystyle p(t)}$ beschrieben und ist das Produkt der reellen Momentanwerte von Spannung und Strom. Bei Verwendung der Kosinus-Schreibweise für die reellen Signale wird damit

${\displaystyle p(t)=u(t)\cdot i(t)=\mathrm {Re} \ {\underline {u}}\;\cdot \;\mathrm {Re} \ {\underline {i}}}$

Aufgrund der Beziehung ${\displaystyle \mathrm {Re} \ {\underline {a}}={\frac {1}{2}}({\underline {a}} {\underline {a}}^{\star })}$ für komplexe Zahlen kann man schreiben

${\displaystyle p(t)={\frac {1}{4}}({\underline {u}} {\underline {u}}^{\star })\cdot ({\underline {i}} {\underline {i}}^{\star })={\frac {1}{4}}({\underline {u}}\;{\underline {i}}^{\star } {\underline {u}}^{\star }\;{\underline {i}}\ {\underline {u}}\;{\underline {i}} {\underline {u}}^{\star }\;{\underline {i}}^{\star })}$

und nach dem Umordnen wieder als Realteil formulieren

${\displaystyle p(t)={\frac {1}{2}}\mathrm {Re} \ ({\underline {u}}\ {\underline {i}}^{\star } {\underline {u}}\ {\underline {i}})={\frac {1}{2}}\mathrm {Re} \left({\hat {u}}\ {\hat {\imath }}\ \mathrm {e} ^{\mathrm {j} (\varphi _{u}-\varphi _{i})} {\hat {u}}\ {\hat {\imath }}\ \mathrm {e} ^{\mathrm {j} (2\omega t \varphi _{u} \varphi _{i})}\right)}$

sowie komplexe Effektivwerte einführen

${\displaystyle p(t)=\mathrm {Re} \left({\underline {U}}\ {\underline {I}}^{\star } {\underline {U}}\ {\underline {I}}\ \mathrm {e} ^{\mathrm {j} 2\omega t}\right)=\mathrm {Re} \left({\underline {U}}\ {\underline {I}}^{\star } {\underline {U}}\ {\underline {I}}^{\star }\ \mathrm {e} ^{\mathrm {j} 2(\omega t \varphi _{i})}\right)=\mathrm {Re} \left[{\underline {U}}\ {\underline {I}}^{\star }\left(1 \mathrm {e} ^{\mathrm {j} 2(\omega t \varphi _{i})}\right)\right]}$

Daraus ergibt sich schließlich der fundamentale Zusammenhang zwischen Momentanleistung und komplexer Leistung:

${\displaystyle p(t)=\mathrm {Re} \left[{\underline {S}}\cdot \left(1 \mathrm {e} ^{\mathrm {j} 2(\omega t \varphi _{i})}\right)\right]}$

Damit ist eine Analyse der Momentanleistung möglich, ohne dass die Additionstheoreme der Kreisfunktionen genutzt werden.

Analyse der Momentanleistung

Indem man den Realteil des Produkts bildet

${\displaystyle p(t)=\mathrm {Re} \left({\underline {S}}\right)\cdot \mathrm {Re} \left(1 \mathrm {e} ^{\mathrm {j} 2(\omega t \varphi _{i})}\right)-\mathrm {Im} \left({\underline {S}}\right)\cdot \mathrm {Im} \left(1 \mathrm {e} ^{\mathrm {j} 2(\omega t \varphi _{i})}\right)}$

und anschließend die Real- bzw. Imaginärteilbildung konkret ausführt, ergibt sich schließlich die aus klassischen Leistungsberechnung (unter Verwendung der Kosinus-Schreibweise für die reellen Signale) bekannte Formel

${\displaystyle p(t)=P\cdot \left(1 \cos {2(\omega t \varphi _{i})}\right)-Q\cdot \sin {2(\omega t \varphi _{i})}}$

Deren Komponenten können wie folgt interpretiert werden:

1. Die Summe beider Komponenten ${\displaystyle p(t)}$ ist die gesamte Momentanleistung (im Diagramm als Kurve 1 gekennzeichnet). Sie schwingt mit der doppelten Grundfrequenz um ihren Mittelwert, der gleich der Wirkleistung ${\displaystyle P}$ ist, und besitzt eine Amplitude in der Größe der Scheinleistung ${\displaystyle S=\left|{\underline {S}}\right|}$.
2. Die rechte Komponente der Momentanleistung (im Diagramm als Kurve 2 gekennzeichnet) ist ebenfalls mit der doppelten Grundfrequenz alternierend. Ihr zeitlicher Mittelwert ist gleich ${\displaystyle 0}$ und ihre Amplitude gleich dem Betrag der Blindleistung ${\displaystyle |Q|}$. Die durch diese Leistung repräsentierte Energie fließt also „immer abwechselnd in gleicher Menge“ zwischen Generator- und Lastzweipol in beiden Richtungen hin und her und kann deshalb im zeitlichen Mittel keine Wirkung ausüben. Aufgrund ihrer Definition wird bei Annahme des Verbraucherzählpfeilsystems positive Blindleistung im Allgemeinen von Induktivitäten, negative Blindleistung von Kapazitäten hervorgerufen. In der Praxis spricht man davon, dass Induktivitäten „Blindleistung beziehen“ und Kapazitäten „Blindleistung liefern“.
3. Die linke Komponente der Momentanleistung (im Diagramm als Kurve 3 gekennzeichnet) besteht (wegen ${\displaystyle 2\cos ^{2}\alpha =1 \cos 2\alpha }$) aus „${\displaystyle \cos ^{2}}$-Schwingungen“ (sinusförmig mit der doppelten Grundfrequenz schwingend), welche von ${\displaystyle 0}$ bis ${\displaystyle 2\;P}$ ansteigen und damit die doppelte Höhe der Wirkleistung haben, wobei ihr zeitlicher Mittelwert (im Diagramm gestrichelt gezeichnet) ebenfalls gleich ${\displaystyle P}$ ist. Die durch diese Leistung repräsentierte Energie fließt also immer in der gleichen Richtung und kann deshalb (im zeitlichen Mittel) eine „tatsächliche Wirkung“ im Lastzweipol (z. B. Erwärmung oder mechanische Arbeit) ausüben. Die Wirkleistung ${\displaystyle P}$ ist also die Amplitude der „tatsächlich wirkenden“ Komponente der Momentanleistung und gleichzeitig ihr zeitlicher Mittelwert. Da die Wirkleistung um den Faktor ${\displaystyle \cos \varphi }$ gegenüber der Scheinleistung geringer ist, nennt man ${\displaystyle \cos \varphi }$ den Wirkfaktor (manchmal auch Leistungsfaktor). Eine negative Wirkleistung deutet auf einen „rückwärtigen (der Bezugsrichtung entgegen gerichteten) Energietransport“ hin. Dieser Fall tritt auf, wenn im Verbraucherzählpfeilsystem der Zweipol als (aktiver) Generator wirkt oder ein passiver Zweipol im Erzeugerzählpfeilsystem beschrieben wird.

Auf Basis dieser Analyse und der grafischen Darstellung kann man auch folgende Aussagen über Wirk- und Blindenergie machen:

• Die Wirkenergie, die während der Dauer einer Periode ${\displaystyle T}$ in den Zweipol fließt oder von ihm abgegeben wird, hat den Betrag ${\displaystyle W_{P}=|P|\cdot T}$.
• Der Flächeninhalt einer Halbschwingung des Verlaufs der Blindleistung repräsentiert die „gesamte hin und her pendelnde Energie“ ${\displaystyle W_{Q}}$. Da der Flächeninhalt einer Sinushalbschwingung bekanntlich ${\displaystyle 2}$ ist, ergibt sich für diesen Energieanteil ${\displaystyle W_{Q}=|Q|\cdot {\frac {T}{2\pi }}={\frac {|Q|}{\omega }}}$.

Beispielsweise erhält man für die „pendelnde Energie“ eines Kondensators mit der Kapazität ${\displaystyle C}$ an einer Spannung mit der Amplitude ${\displaystyle {\hat {u}}}$ und der Kreisfrequenz ${\displaystyle \omega }$ entsprechend der oben angegebenen Blindleistung

${\displaystyle W_{Q}={\frac {{\hat {u}}^{2}\cdot \omega \ C}{2\ \omega }}={\frac {{\hat {u}}^{2}\cdot C}{2}}}$

Das ist aber gerade die bekannte Energie eines auf die Spannung ${\displaystyle {\hat {u}}}$ aufgeladenen Kondensators.

Literatur

• Klaus Lunze: Theorie der Wechselstromschaltungen. 8. Auflage. Verlag Technik GmbH, Berlin 1991, ISBN 3-341-00984-1. 
• Reinhold Paul: Elektrotechnik 2 – Netzwerke. Springer-Verlag, Berlin Heidelberg New York 1994, ISBN 3-540-55866-7.