Mollweide-Projektion

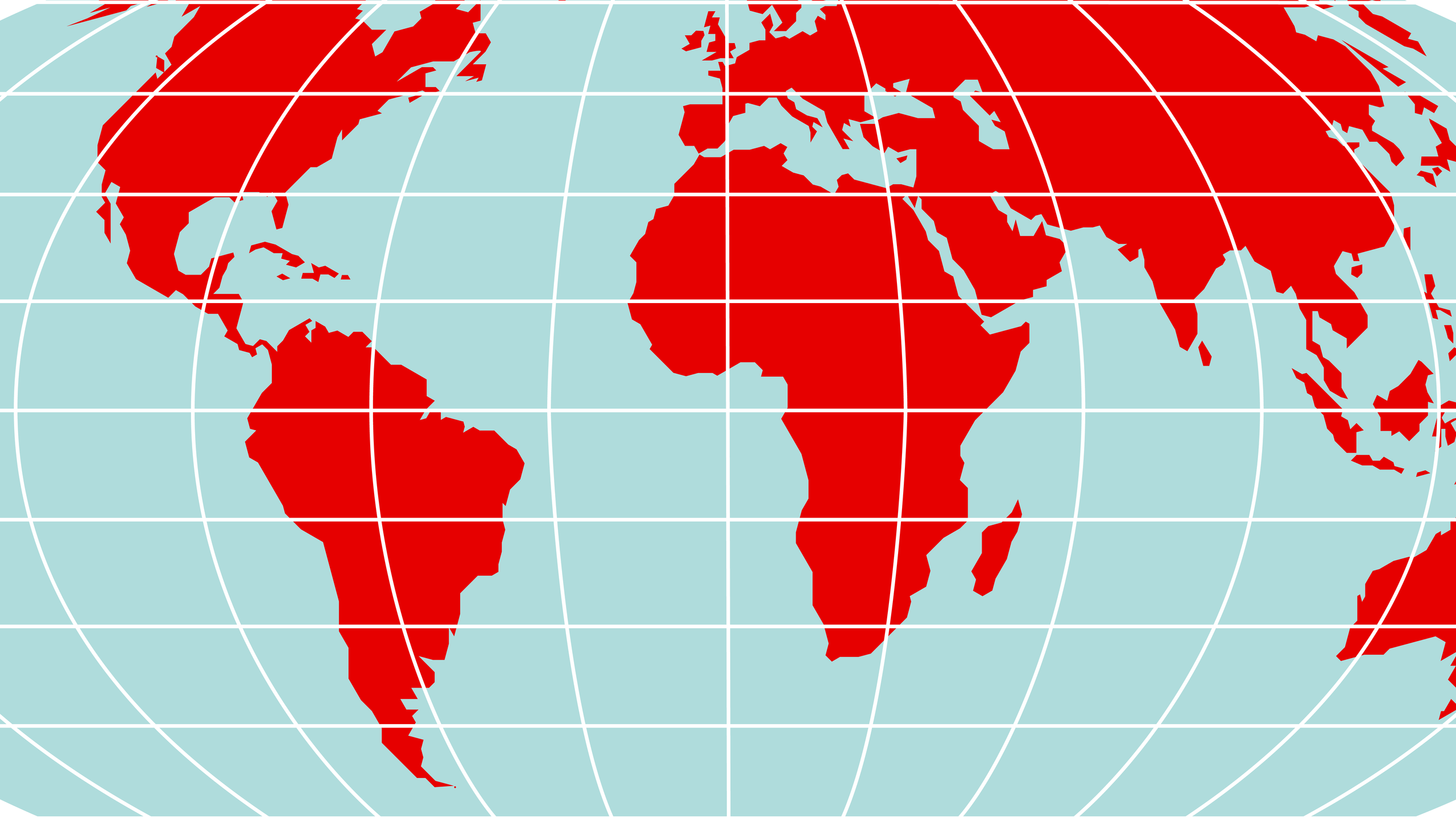
Die Mollweide-Projektion ist eine von Carl Brandan Mollweide entwickelte und 1805 veröffentlichte flächentreue Kartenprojektion, welche die gesamte Erdoberfläche als Ellipse darstellt.

Äquator und Mittelmeridian (oft der Nullmeridian) werden maßstabsgetreu als Geraden wiedergegeben. Breitenkreise werden als Geraden dargestellt, Meridiane als Ellipsen. Der dem Mittelmeridian gegenüberliegende Meridian bildet den Außenrand der Karte. Die Meridiane, welche um ±90° vom Mittelmeridian versetzt sind, bilden einen Kreis. Die Verzerrung nimmt mit zunehmendem Abstand vom Äquator und Mittelmeridian sehr stark zu.

Die ähnlich aussehende Hammer-Aitov-Projektion besitzt geringere Winkelverzerrungen und ist somit anschaulicher, dafür ist sie aufwändiger zu rechnen. Andererseits hat diese keine geradlinig-parallelen Breitenkreise, was beispielsweise für Zonenmodelle ungünstig ist. Daher ist die Mollweide-Projektion besonders für klimatologische, biologische und ähnliche Themenkarten weit verbreitet.

Es gibt eine zerlappte, flächen- und lagetreue Form nach J. P. Goode, die Goode-Homolosine-Projektion.

Transformation

Die Mollweide-Projektion lässt sich durch folgende Formeln beschreiben:

${\displaystyle {\begin{aligned}x&=R{\frac {2{\sqrt {2}}}{\pi }}\left(\lambda -\lambda _{0}\right)\cos \theta ,\\[5px]y&=R{\sqrt {2}}\sin \theta ,\end{aligned}}}$

Dabei bezeichnen ${\displaystyle R}$ den Erdradius, ${\displaystyle \lambda }$ die Länge, ${\displaystyle \lambda _{0}}$ die Länge des Zentralmeridians und ${\displaystyle \varphi }$ die Breite. ${\displaystyle \theta }$ ist ein Hilfswinkel, der durch die Gleichung

${\displaystyle 2\theta \sin 2\theta =\pi \sin \varphi \qquad (1)}$

festgelegt ist; diese transzendente Gleichung lässt sich mithilfe des Newton-Verfahrens lösen.

Die Karte hat den Flächeninhalt ${\displaystyle 4\pi R^{2}}$, wenn die gesamte Erdoberfläche dargestellt wird. Die x-Koordinate kann Werte zwischen ${\displaystyle -2R{\sqrt {2}}}$ und ${\displaystyle 2R{\sqrt {2}}}$ haben, die y-Koordinate Werte zwischen ${\displaystyle -R{\sqrt {2}}}$ und ${\displaystyle R{\sqrt {2}}}$.

Die Umkehrformeln lauten

${\displaystyle {\begin{aligned}\varphi &=\arcsin {\frac {2\theta \sin 2\theta }{\pi }},\\[5px]\lambda &=\lambda _{0} {\frac {\pi x}{2R{\sqrt {2}}\cos \theta }}\end{aligned}}}$

mit

${\displaystyle \theta =\arcsin {\frac {y}{R{\sqrt {2}}}}.\,}$

Ähnliche Projektionen:

Beispiele

Einzelnachweise

Weblinks

• Eric W. Weisstein: Mollweide Projection. In: MathWorld (englisch).